第一章 引言

什么是被动攻击和主动攻击,各有几种类型?

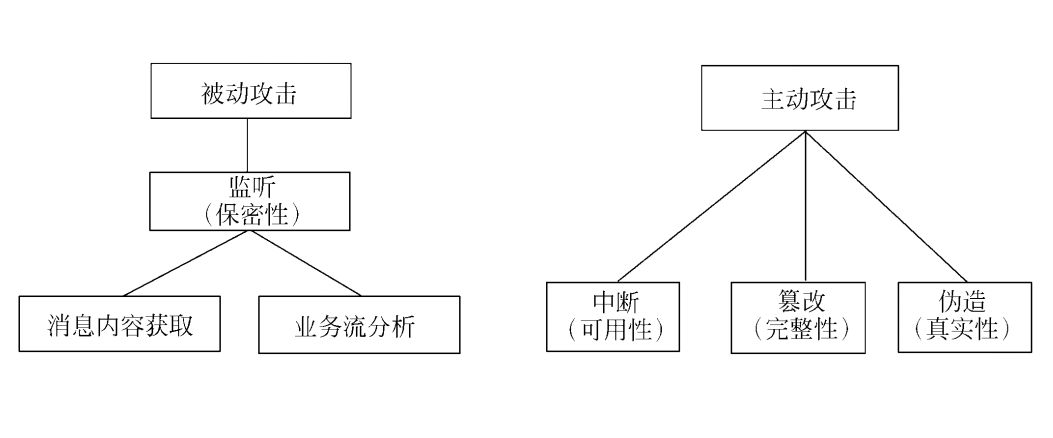
  • 被动攻击：也称窃听，以获取信息为目的。 仅攻击信息的保密性，不影响正常的网络通信，不对消息作任何修改 搭线窃听、对文件或程序非法复制、木马、对资源的非授权使用 被动攻击又分为两类：获取消息的内容和业务流分析

    • 获取消息的内容：通过破译密文等手段直接获取机密信息的内容
    • 业务流分析：敌手虽然可能无法从截获的消息中获取内容，但却有可能获知消息的长度，格式，通信双方的位置和身份，通信次数。在商业环境，用户隐私，以及军网中这些消息可能是敏感的。

  • 主动攻击：对数据流进行篡改或产生假的数据流 可分为3类：

    • 中断：对系统可用性进行攻击 破坏计算机硬件，网络，或文件管理系统。如DoS，病毒等
    • 篡改：对完整性进行攻击 修改文件中的数据(数据修改后存储)，替换某一程序使其执行不同功能 修改网络中传送消息的内容等，比如中间节点对转发的图象进行了压缩
    • 伪造：对真实性进行攻击 在网络中插入伪造的消息冒充消息发送者，在文件中插入伪造记录等

分别是对信息系统的什么性质进行的攻击?

image-20201202223722440

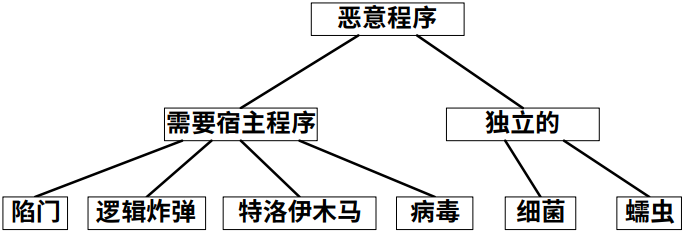
恶意程序的分类

  • 根据是否需要宿主程序及是否可以自我复制可分为病毒、蠕虫、特洛伊木马、逻辑炸弹等

image-20201202223932943

安全业务分为哪五种?各自含义

  • 保密业务,防止被动攻击
    • 机密性就是保护信息（数据）不泄露或不泄露给那些未授权掌握这一信息的实体，如防止消息内容泄漏，被窃听。
    • 在信息系统安全中需要区分两类机密性服务：
      • 数据机密性服务：使攻击者想要从某个数据项中推出敏感信息是十分困难的
      • 业务流机密性服务：使攻击者想要通过观察通信系统的业务流来获得敏感信息是十分困难的如防止敌手进行业务流分析，以获得信源，信宿，次数，消息长度等
  • 认证业务
    • 鉴别是最基本的安全服务，是对付假冒攻击的有效方法，以保障通信的真实性，鉴别可以分为对等实体鉴别和数据源鉴别 (1) 对等实体鉴别， 即身份认证，如主机和终端，主机和服务器等。保障身份的真实性，通信双方都相信对方是真实的，这种服务可以是单向的，也可以是双向的，可以带有有效期检验，也可以不带。 (2) 数据源鉴别，保障通信连接的真实性，通信连接不能被第三方介入，以假冒其中的一方而进行非授权的传输或接受。单向通信：认证业务功能是使接收者相信消息确实是由它自己所声称的那个信源发出的。
  • 完整性业务
    • 完整性服务用于对抗数据在存储、传输等处理过程中受到的非授权修改 ，如用于消息流：保证所接收的消息未经复制、插入、篡改、重排、或重放。即保证接收的消息和发送的消息完全一样 和机密性一样可以实现不同粒度的完整性保护
    • 还能用于一定程度上对已经毁坏的数据进行恢复
  • 不可否认性业务
    • 用于防止通信双方中的某一方对所传送的消息的否认，保护通信实体免遭来自其他合法实体的威胁
    • 一个消息发出后，接收者能够证明消息的真实来源，发送者能够证明接收者确已接收了该消息
  • 访问控制
    • 访问控制用于防止资源的未授权使用，控制的实现方式是认证，检查用户是否有对某一资源的访问权

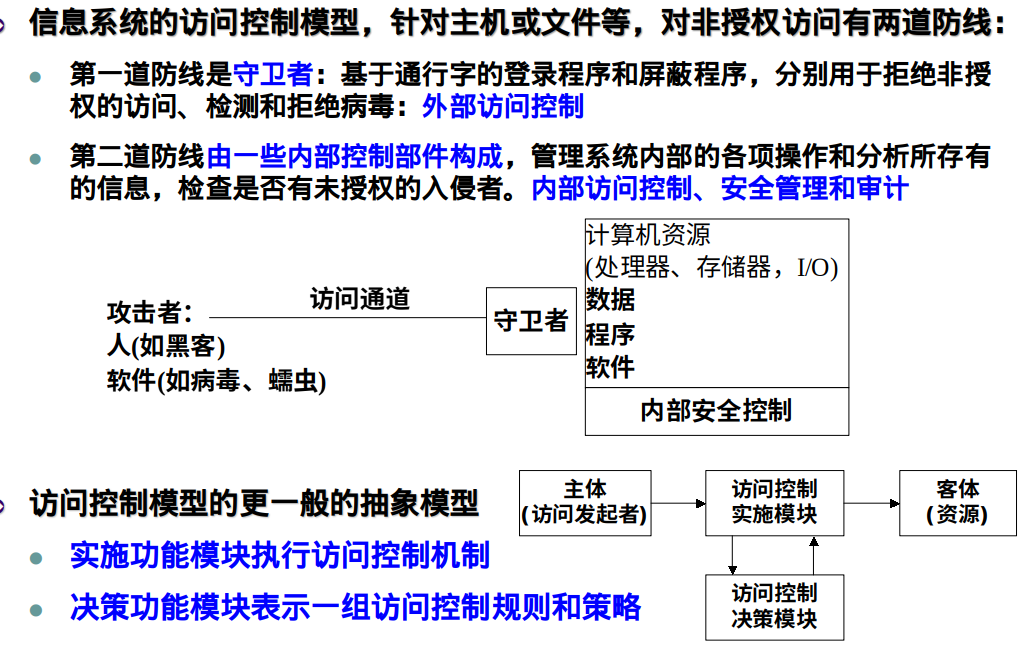
信息安全的基本模型?信息系统的保护模型?

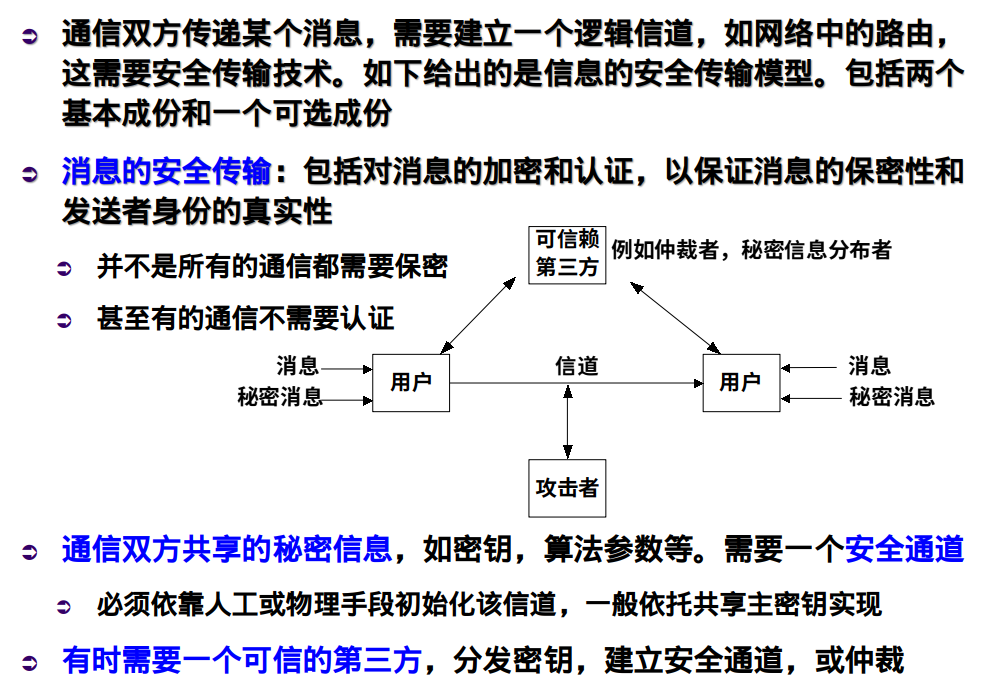
image-20201203000641980

image-20201203000706297

image-20201203000603489

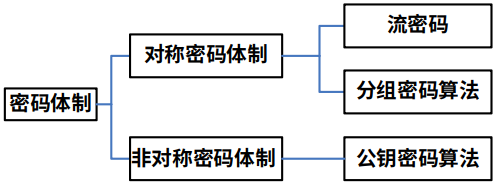
密码体制从原理上可分为哪两大类?含义

  • 单钥体制
    • 传统密码体制所用的加密密钥和解密密钥相同k1＝k2，称为单钥密码体制，也称为对称密码体制
  • 双钥密码体制
    • 加密密钥和解密密钥不相同，称为双钥密码体制，也称为非对称密码体制或公钥体制

单钥密码体制对明文加密的两种方式?

image-20201203001638672

  • 流密码
    • 明文消息按字符或比特逐位加密
    • 需要一个至少和明文一样长的密钥流
  • 分组密码
    • 将明文消息分组(含有多个字符)，逐组进行加密
    • 用同一个密钥分别对不同的分组按照一定的运行模式加密

对密码体制的攻击的4种类型

  • 唯密文攻击

  • 已知明文攻击

  • 选择明文攻击

  • 选择密文攻击

  • 攻击类型攻击者掌握的内容
    惟密文攻击加密算法，截获的部分密文
    已知明文攻击加密算法，截获的部分密文，一个或多个明密文对
    选择明文攻击加密算法，截获的部分密文，自己选择的明文消息及由密钥产生的相应密文
    选择密文攻击加密算法，截获的部分密文，自己选择的密文消息及相应的被解密的明文

第二章 流密码

密码和流密码的区别? 同步流密码的概念

分组密码与流密码的区别在于 有无记忆性 ,流密码的滚动密钥 $z_0=f(k,\theta_0)$ , 由函数 $f$ , 密钥 $k$, 和指定的初态 $\theta_0$ 完全确定. 此后,由输入加密器的明文可能影响加密器中内部记忆部件的存储状态,因而 $\theta_i (i>0)$ 可能依赖于 $k, \theta_0, x_0, x_1,…,x_{i-1}$ 等参数.

根据加密器中的记忆元件的储存状态 $\theta_i$ 是否依赖于输入的明文字符,流密码可以进一步分成同布和自同步两种. $\theta_i$ 独立于明文字符的叫同步流密码,否则叫自同步流密码.

有限状态自动机的基本原理

有限状态自动机是具有离散输入和输出（输入集和输出集均有限）的一种数学模型，由以下3部分组成：

image-20201203002501254

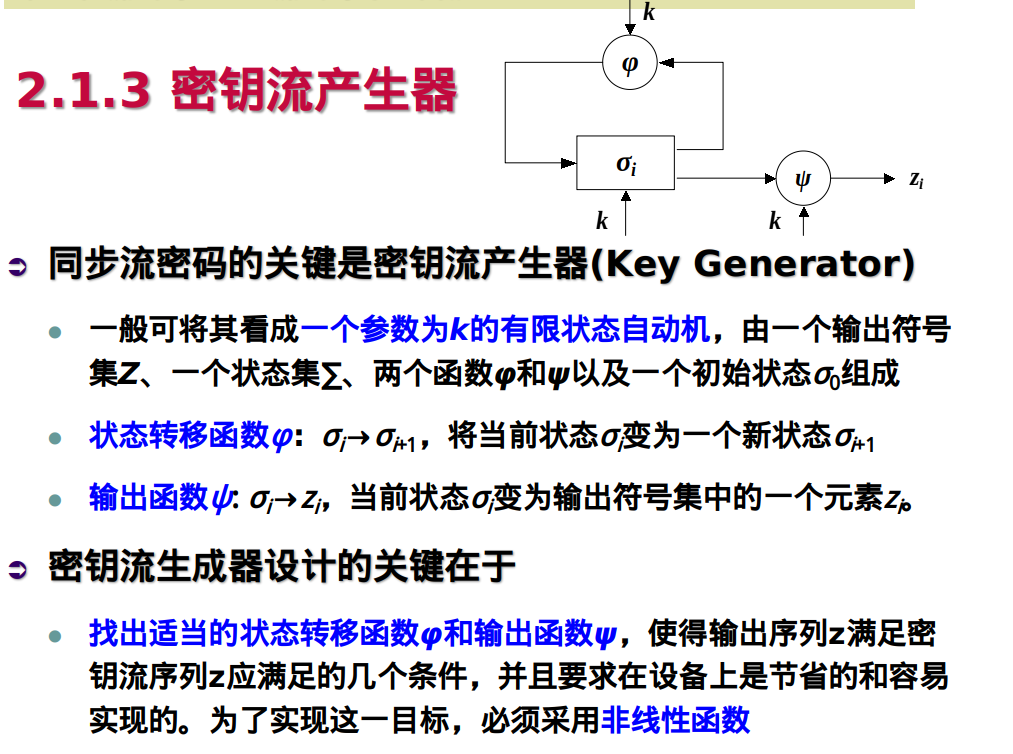
密钥流生成器的分解和常见的密钥流生成器

image-20201203002542525

LFSR输出序列和周期的计算

image-20201203002708565

LFSR的特征多项式及其性质

image-20201203130654011

  • 记$2^n-1$个非零序列的全体为G(p(x))。
  • 定理2-2 p(x)|q(x)的充要条件是G(p(x))属于G(q(x))
  • 说明可用n级LFSR产生的序列，也可用级数更多的LFSR来产生
  • 若序列{ai}的特征多项式p(x)定义在GF(2)上，p是p(x)的周期，则{ai}的周期r|p。
  • 说明n级LFSR输出序列的周期r不依赖于初始条件，而依赖于特征多项式p(x)。
  • 初始状态对序列的周期有一定的影响
  • 所有这些m序列之间是相互移位的关系，本质上是同一个序列

m序列密码的条件和破译

  • n级LFSR产生的序列有最大周期的必要条件是其特征多项式为不可约的
  • 注意：只要有一条序列为m序列，则所有非0序列都是m序列
  • 该定理的逆不成立，即LFSR的特征多项式为不可约多项式时，其输出序列不一定是m序列。
  • 若n次不可约多项式p(x)的阶为$2^n-1$，则称p(x)是n次本原多项式
  • {ai}为m序列的充要条件是p(x)为本原多项式。
  • 对于任意的正整数n，至少存在一个n次本原多项式
  • m序列虽然具有最大的周期，然而因它是线性序列而极其不安全，只要知道连续的2n个bit的序列就可以完全破译了。即可以求出m序列产生器特征多项式的n个系数
  • image-20201203132132165
  • image-20201203132408685

第三章 分组密码体制

  • 与流密码相比无记忆性。在相同密钥下分别对长为n的输入明文组实施相同变换，所以只需研究对任一组明文数字的变换规则。
  • 分组密码实质上是字长为n的数字序列的代换密码
  • 分组密码的优缺点
    • 适合软硬件实现，软件实现及标准化优于流密码
    • 没有有效的数学工具，安全性一般无法证明

Shannon提出的设计密码系统的两个基本方法

  • 扩散和混淆(diffusion and confusion)是由Shannon提出的设计密码系统的两个基本准则，目的是抗击敌手对密码系统的统计分析

  • 扩散性：所设计的密码应使得

    • (1) 密钥的每一个比特影响密文的每一个比特，以防止对密钥进行逐段破译；
    • (2) 明文的每一个比特影响密文的每一个比特，以便最充分地隐蔽明文。即将明文的统计特性散布到密文中去，从而使明文和密文之间的统计关系变得尽可能复杂

  • 混淆性：

    • 是使密文和密钥之间的统计关系变得尽可能复杂，以使敌手无法得到密钥。 即使敌手能得到密文的一些统计关系，由于密钥和密文之间的统计关系复杂化，敌手也无法得到密钥。
    • 使用复杂的代换算法可以得到预期的混淆效果 简单的线性代换函数得到的混淆效果则不够理想

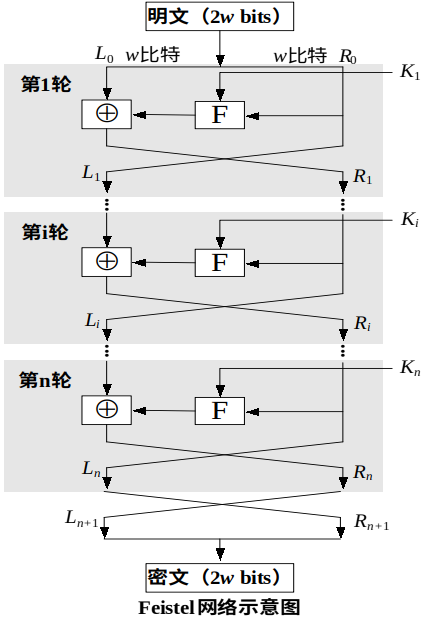
Feistel网络的加解密结构

image-20201203103903529

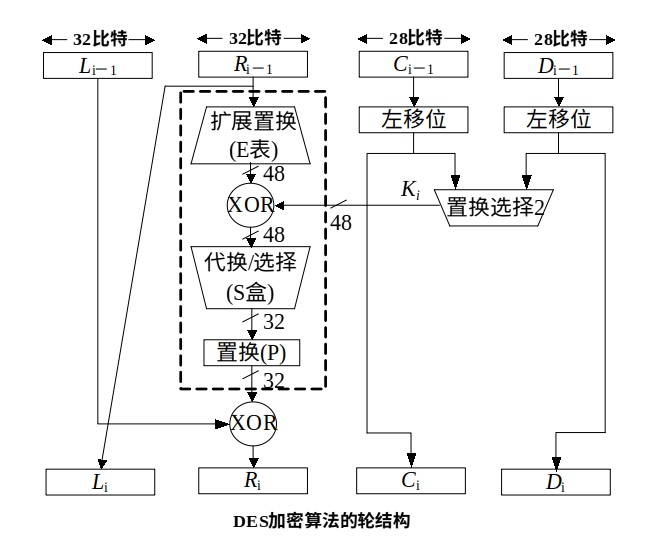
DES加密算法的基本原理和过程

image-20201203103942849

image-20201203104041847

分组密码的四种运行模式和用途

模式描述用途
电码本(ECB)模式每个明文组独立地以同一密钥加密传送短数据(如一个加密密钥)
密码分组链接(CBC)模式加密算法的输入是当前明文组与前一密文组的异或传送数据分组；认证
密码反馈(CFB)模式每次只处理输入的j比特，将上一次的密文作加密算法的输入以产生伪随机输出，该输出再与当前明文异或以产生当前密文传送数据流；认证
输出反馈(OFB)模式与CFB类似不同之处是本次加密算法的输入为前一次加密算法的输出有扰信道上(如卫星通信)传送数据流
计数器(CTR)模式对计数器依次用k加密后与明文异或适合并行，可随机访问

IDEA算法的基本原理和过程

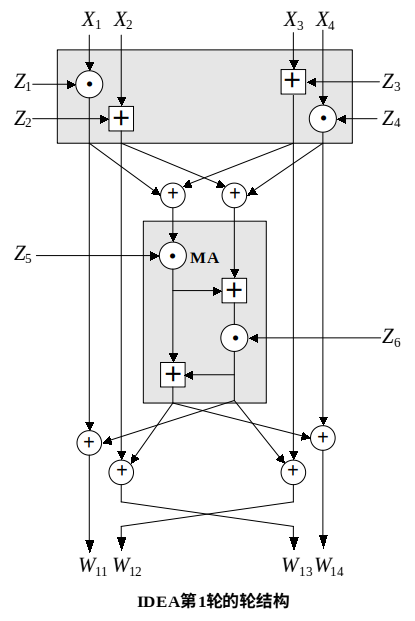
image-20201203152343813

  • 每轮开始时有一个变换，该变换的输入是4个子段和4个子密钥 变换中的运算是两个乘法和两个加法 输出的4个子段经异或运算形成了两个16比特的子段作为MA结构的输入 MA结构也有两个输入的子密钥，输出是两个16比特的子段 最后，变换的4个输出子段和MA结构的两个输出子段经过异或运算产生这一轮的4个输出子段

AES算法的原理和过程

  • Rijndael的轮函数由4个不同的计算部件组成，分别是： 字节代换（ByteSub）、行移位（ShiftRow） 列混合（MixColumn）、密钥加（AddRoundKey）
  • 轮函数的伪C代码如下： Round (State, RoundKey) { ByteSub (State); ShiftRow (State); MixColumn (State); AddRoundKey (State, RoundKey) }
  • 结尾轮的轮函数与前面各轮不同，将MixColumn这一步去掉。其伪C代码如下： FinalRound (State, RoundKey) { ByteSub (State); ShiftRow (State); AddRoundKey (State, RoundKey) }
  • “InvShiftRow”与“InvByteSub”两个计算部件可以交换顺序
  • Rijndael密码的解密算法为顺序完成以下操作：初始的密钥加；(Nr-1)轮迭代；一个结尾轮。其中解密算法的轮函数为 InvRound (State, RoundKey) { InvByteSub (State); InvShiftRow (State); InvMixColumn (State); AddRoundKey (State, RoundKey) } 解密算法的结尾轮为 InvFinalRound (State, RoundKey) { InvByteSub (State); InvShiftRow (State); AddRoundKey (State, RoundKey) }

第四章 公钥密码

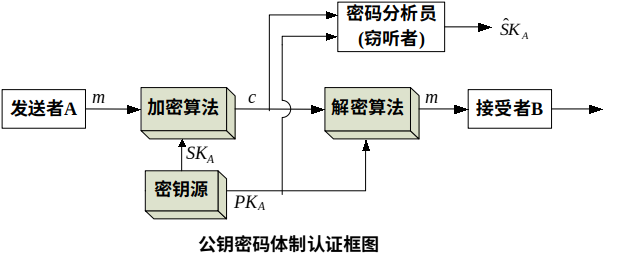
公钥密码体制的加密和认证原理

  • 公钥密码算法基本工具不再是代换和置换，而是数学函数

  • 以非对称的形式使用两个密钥，两个密钥的使用对保密性、密钥分配、认证等都有着深刻的意义。

  • 公钥密码算法的最大特点是采用两个相关密钥将加密和解密能力分开

  • 一个密钥是公开的，称为公开密钥，简称公开钥，用于加密、验证签名，可以被任何人知道

  • 另一个密钥是为用户专用，因而是保密的，只能被消息的接收者或签名者知道，称为秘密密钥，简称秘密钥，用于解密、产生签名

  • 因此公钥密码体制也称为双钥密码体制

  • 公钥体制的加密过程: ① 密钥的产生 ：要求接收消息的端系统，产生一对用来加密和解密的密钥$PK_B$和$SK_B$，如图中的接收者B，其中$PK_B$是公开钥，$SK_B$是秘密钥。因此，公钥可以发布给其他人 ② 公开钥的分发 ：B将加密密钥$(PK_B)$予以公开。另一密钥则被保密$(SK_B)$ ③ 加密 ：A要想向B发送消息m，则使用B的公开钥加密m，表示为$ c=E_{PK_B}[m] $其中c是密文，E是加密算法 ④ 解密 ：B收到密文c后，用自己的秘密钥$SK_B$解密，即$m=D_{SK_B}[c]$，其中D是解密算法。因为只有B知道$SK_B$，所以其他人都无法对c解密。

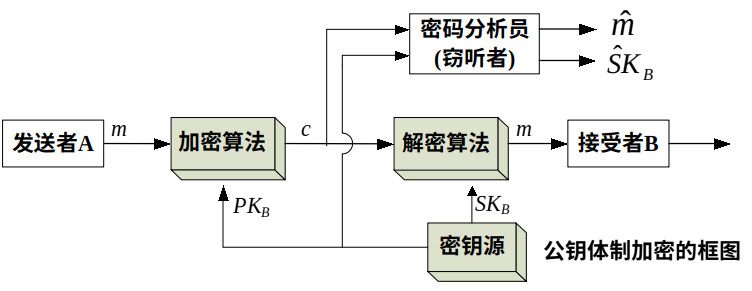
    image-20201201211808966

  • 公钥体制的认证过程

    公钥加密不仅能用于加、解密，还能用于对发方A发送的消息m提供认证 用户A用自己的秘密钥$SK_A$对m加密，表示为$c=E_{SK_A}[m]$ 将c发往B。B用A的公开钥$PK_A$对c解密，表示为$m=D_{PK_A}[c]$ 因为从m得到c是经过A的秘密钥$SK_A$加密，**只有A才能做到**。因此c可当做A对m的**数字签字**。 任何人只要得不到A的秘密钥$SK_A$就不能篡改m，所以以上过程获得了对**消息来源和消息完整性的认证**，也实现了**对身份的认证**。

    image-20201201212628277

RSA加密体制的原理和计算

  • 它既可用于加密、又可用于数字签字。
  • RSA算法的安全性是基于数论中大整数分解的困难性(但可能达不到大数分解的困难强度)
  • 1 密钥的产生 ① 选两个保密的大素数p和q ② 计算n=p×q，$\phi(n)=(p-1)(q-1)$，其中$\phi(n)$是n的欧拉函数值 ③ 选一整数e，满足$1<e< \phi(n)$，且$gcd(\phi(n),e)=1$ ④ 计算$d$，满足$ d * e = 1 \mod \phi(n)$, 即d是e在模$\phi(n)$下的乘法逆元，因e与$\phi(n)$互素，模$\phi(n)$的乘法逆元一定存在 ⑤ 以{e,n}为公开钥,{d,p,q}为秘密钥 秘密钥也可记为d，或{d, n}，如果是系统负责产生密钥，则用户可能不知道p,q
  • 2 加密 加密时首先将明文比特串分组，使得每个分组对应的十进制数小于n，即分组长度小于$log_2 n$。 然后对每个明文分组m，作加密运算： $c≡m^e \mod n$
  • 3 解密 对密文分组的解密运算为： $m≡c^d \mod n$
  • RSA的加密很快，因为加密指数e一般选择得很小 解密指数d很大，需要计算模 300digits (or 1024bits) 的乘法，计算机不能直接处理这么大的数，计算速度很慢，需要考虑其它技术，加速RSA的实现 如果知道p和q，可采用中国剩余定理CRT： CRT 对RSA解密算法生成两个解密方程（利用$M=C^d \mod N$，$N=p * q$）, 即：$M_1 = M \mod p = (C \mod p)^{d \mod (p-1)} \mod p$ $M_2 = M \mod q = (C \mod q)^{d \mod (q-1)} \mod q$ 解方程 $M = M_1 \mod p$ $M = M_2 \mod q $ 具有唯一解（利用CRT ）： $M = M_1 * q * (q^{－1} \mod p) + M_2 * p * (p^{－1} \mod q) \mod N$ 不考虑CRT的计算代价，改进的算法的解密速度是原来的4倍 若考虑CRT的计算代价，改进后的算法解密速度是原来的3倍多
  • RSA密钥的产生 需考虑两个大素数p、q的选取，以及e的选取和d的计算 n(=p*q) 是公开的，为了防止敌手通过穷搜索发现p、q，这两个素数应足够大，且具有好的随机性 (1) 如何有效地寻找大素数 一般是先随机选取一个大的奇数（例如用伪随机数产生器）， 然后用素性检验算法检验这一奇数是否为素数，如果不是则选取另一大奇数，重复这一过程，直到找到素数为止 素性检验算法通常都是概率性的，常用Miller-Rabin概率检测算法实现，只有在产生新密钥时才需执行这一工作 (2) 如何选取满足$gcd(\phi(n),e)=1$的e，并计算满足$d * e≡1 \mod \phi(n)$的d,这一问题可由推广的Euclid算法完成

背包密码体制的原理和计算

  • 设$A=(a_1,a_2,…,a_n)$是由 n 个不同的正整数构成的 n 元组，s 是另一已知的正整数。背包问题就是从 A 中求出所有的 $a_i$，使其和等于 s。其中 A称为背包向量，s 是背包的容积。 例如,A=(43, 129, 215, 473, 903, 302, 561, 1165, 697, 1523)，s=3231。 由于 3231=129+473+903+561+1165 所以从 A 中找出的满足要求的数有129、473、903、561、1165 原则上讲，通过检查 A 的所有子集，总可找出问题的解（若有解的话） 本例 A 的子集共有$2^{10}=1024$个（包括空集）。 然而如果 A 中元素个数 n 很大，子集个数 $2^n$将非常大。 如A中有300个元素，A的子集有$2^{300}$。寻找满足要求的 A 的子集没有比穷搜索更好的算法，因此背包问题( Knapsack)是NPC问题

  • 由背包问题构造公钥密码体制同样是要构造一个(陷门)单向函数f 将 $x (1≤x≤2 * n-1)$ 写成长为 n 的二元表示, f(x) 定义为 A 中所有$a_i$的和，其中 x 的二元表示的第 i 位为1，即 $f(1)=f(0…001)=a_n;$

    $f(2)=f(0…010)=a_{n-1};$

    $ f(3)=f(0…011)=a_{n-1}+a_n;$

    $f(2n-1)=f(1…111)=a_1+a_2+…+a_n$

    使用向量乘(内积)，有$f(x)=A·B_x$，其中$B_x$是x二元表示的列向量。 上例中f(364) =f(0101101100)= 129+473+903+561+1165 = 3231 显然，已知 x 很容易求 f(x)，但已知 f(x) 求 x 就是要解背包问题。 为使接收方能够解密，就需找出单向函数 f(x) 的陷门。为此需引入一种特殊类型的背包向量。

  • 定义背包向量$A=(a_1,a_2,…,a_n)$称为超递增的，如果 $a_j > a_1+a_2+…+a_{j-1}, 其中j=1,2,3…n$

  • 超递增背包向量对应的背包问题很容易通过以下算法求解。 已知 s 为背包容积，对A从右向左检查每一元素，以确定是否在解中。 若 $s≥a_n$，则 $a_n$ 在解中，令 $x_n=1$； 若 $s < a_n$，则 $a_n$ 不在解中，令$x_n=0$。 下面令

    s = s if s<a[i] else s-a[i]

    对$a_{n-1}$重复上述过程，一直下去，直到检查出$a_1$是否在解中。 检查结束后得 $x=(x_1x_2…x_n)$，$B_x=(x_1x_2…x_n)^T$

  • 1 密钥产生 选一个超递增背包向量 $ A=(a_1,a_2,…,a_n) $ 用模乘对 A 进行伪装，模乘的模数 k 和乘数 t 皆取为常量，满足 ，gcd(t, k) = 1，即 t 在模 k 下有乘法逆元。 设 $b_i≡t·a_i \mod k$, i=1,2,…,n，得一新的背包向量$ B = (b_1,b_2,…,b_n)$，记为 $B≡t · A \mod k$ 用户以 B 作为自己的公开钥，A, t, k为私钥

  • 2.加密 对明文分组 $x=(x_1x_2…x_n)$的加密运算为$c=f(x)=B·B_x \mod k$

  • 3. 解密 首先由$s≡t^{-1}c \mod k$，求出 s 作为超递增背包向量 A 的容积， 再由超递增背包向量A解背包问题即得$x=(x_1x_2…x_n)$。

  • 过了两年该体制即被破译

Rabin加密体制的原理和计算

  • Rabin密码体制已被证明对该体制的破译等价于对大整数的分解

  • RSA中选取的公开钥e满足$1<e<\phi(n)$，且$gcd(e,\phi(n))=1$。Rabin密码体制则取e=2

  • 1 密钥的产生: 随机选择两个大素数p、q，满足$p≡q≡3 \mod 4$，Blum数，即这两个素数形式为$4 * k+3$；计算$n = p * q$。以 n 作为公开钥，p、q 作为秘密钥。

  • 2. 加密:

    $c≡m^2 \mod n$ 其中 m 是明文分组，c 是对应的密文分组。

  • 3. 解密: 解密就是求c模n的平方根，即解$x^2≡c \mod n$，因此，Rabin体制也被称为基于环上二次剩余困难性构造，由中国剩余定理知解该方程等价于解方程组

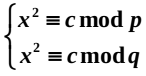
  • image-20201201223418393

  • 由于p≡q≡3 mod 4，方程组的解可容易地求出，其中每个方程都有两个解，即$ x≡\pm m_1 \mod p$， $x≡\pm m_2 \mod q$， 经过组合可得4个同余方程组

  • 由中国剩余定理可解出每一方程组的解，共有4个，即每一密文对应的明文不惟一。为了有效地确定明文,可在 m 中加入某些信息,如发送者的身份号、接收者的身份号、日期、时间等。

  • Rabin密码在选择密文攻击CCA下是不安全的

ElGamal密码体制

  1. 密钥产生 选择一个大的素数 p ；选择 g ，1 < g < p；选择 x，1 < x < p-1； 计算$y = g^x \mod p$，公钥是(p, g, y)，私钥是x
  2. 加密 设欲加密明文消息M，0 < M < p 随机选一整数 k , 满足 gcd(k, p－1) = 1 计算对$C1≡g^k \mod p,C2≡y^kM \mod p$，密文为C = C1||C2 (级联)
  3. 解密 $M=C_2/C_1x \mod p$ 这是因为$C_2/C_1^x \mod p＝y^kM/g^{kx} \mod p＝y^kM/y^k \mod p＝M \mod p $ 特点：密文由明文和所选随机数k来定，因而是一种概率加密体制代价是使数据扩展一倍

Diffie-Hellman 密钥交换

  • 算法的唯一目的是使得两个用户能够安全地交换密钥，得到一个共享地会话密钥，算法本身不能用于加、解密

  • 算法的安全性基于求离散对数的困难性

  • 假设 p 是大素数， g 是 p 的本原根，p 和 g 作为公开元素，协议如下： ① 用户Alice选择随机数x，计算 $a=g^x \mod p$，保密x，发送a给Bob ② 用户Bob选择随机数y，计算 $b=g^y \mod p$，保密y，发送 b 给Alice ③ Bob和Alice各自计算 $k=b^x \mod p$ 和 $k=a^y \mod p$, 从而得到共享密钥 k 这是因为$k=b^x mod p=(g^y)^x \mod p=(g^x)^y \mod p=a^y \mod p$

ECC加密体制的原理和优点

  • 与基于有限域上离散对数问题的公钥体制（如Diffie-Hellman密钥交换和ElGamal密码体制）相比，椭圆曲线密码体制有如下优点:

  • 1: 安全性高

    攻击有限域上的离散对数问题可以用指数积分法，对椭圆曲线上的离散对数问题并不有效。 目前攻击椭圆曲线上的离散对数问题的方法只有适合攻击任何循环群上离散对数问题的大步小步法

  • 2: 密钥量小

    由攻击两者的算法复杂度可知，在实现相同的安全性能条件下，椭圆曲线密码体制所需的密钥量远比基于有限域上的离散对数问题的公钥体制的密钥量小

  • 3: 灵活性好

    有限域GF(q)一定的情况下，其上的循环群（即GF(q)-{0}）就定了 GF(q)上的椭圆曲线可以通过改变曲线参数，得到不同的曲线，形成不同的循环群。因此，椭圆曲线具有丰富的群结构和多选择性 可在保持和RSA/DSA体制同样安全性能的前提下大大缩短密钥长度(目前160比特足以保证安全性)，因而在密码领域有着广阔的应用前景

ECC上的Elgamal密码体制

  • 椭圆曲线并非椭圆，之所以称为椭圆曲线是因为它的曲线方程与计算椭圆周长的方程类似。一般来讲，椭圆曲线的曲线方程是以下形式的三次方程： $y^2+axy+by=x^3+cx^2+dx+e$
    其中a，b，c，d，e是满足某些简单条件的实数。定义中包括一个称为无穷点的元素，记为O。

  • 椭圆曲线关于x轴对称。

  • 3个点位于同一直线上，那么它们的和为O

  • O为加法单位元，即对椭圆曲线上任一点P，有 P+O=P

  • 设P1=(x,y)是椭圆曲线上的一点（如图所示），它的加法逆元定义为P2=－P1=(x, -y)

  • 设Q和R是椭圆曲线上x坐标不同的两点，Q+R的定义如下： 画一条通过Q、R的直线与椭圆曲线交于P1

    由Q+R+P1=O 得 Q+R=-P1

  • 点Q的倍数定义如下： 在Q点做椭圆曲线的一条切线，设切线与椭圆曲线交于点S，定义2Q=Q+Q=-S。类似地可定义3Q=Q+Q+Q+，…，

  • 以上定义的加法具有加法运算的一般性质，如交换律、结合律等

  • image-20201203003849614

  • image-20201203003904391

  • (0，1)(0，22)(1，7)(1，16)(3，10)(3，13)(4，0)(5，4)(5，19)
    (6，4)(6，19)(7，11)(7，12)(9，7)(9，16)(11，3)(11，20)(12，4)
    (12，19)(13，7)(13，16)(17，3)(17，20)(18，3)(18，20)(19，5)(19，18)

    image-20201203004552592

    image-20201203004700143

    image-20201203004848194

  • image-20201203003503148

第五章 密钥分配与密钥管理

  • 密钥的种类与使用周期 密钥加密密钥(key encrypting key):在传输会话密钥时，用来加密会话密钥的密钥称为密钥加密密钥，也称次主密钥(submaster key)或二级密钥(secondary key) 主机主密钥(host master key):对密钥加密密钥进行加密的密钥称为主机主密钥。它一般保存于网络中心、主节点、主处理机中，受到严格的物理保护。一般在密钥分配中心以及终端系统中主密钥都是物理上安全的。如果主密钥泄露了，则相应的会话密钥也将泄露，如果把主密钥当作会话密钥注入加密设备，那么其安全性则降低
  • 两个用户（主机、进程、应用程序）在用单钥密码体制进行保密通信时，首先必须有一个共享的秘密密钥，为防止攻击者得到密钥，还必须时常更新密钥。因此，密码系统的强度也依赖于密钥分配技术
  • 两个用户A和B获得共享密钥的方法有以下4种： ① 密钥由A选取并通过物理手段发送给B ② 密钥由第三方选取并通过物理手段发送给A和B ③ 如果A、B事先已有一密钥，则其中一方选取新密钥后，用已有的密钥加密新密钥并发送给另一方 ④ 如果A和B与第三方C分别有一保密信道，则C为A、B选取密钥后，分别在两个保密信道上发送给A、B
  • 第1和第2种方法称为人工发送 在通信网中，若只有个别用户想进行保密通信，密钥的人工发送还是可行的。然而如果所有用户都要求支持加密服务，则任意一对希望通信的用户都必须有一共享密钥。如果有n个用户，则密钥数目为n(n-1)/2。因此当n很大时，密钥分配的代价非常大，密钥的人工发送是不可行的 系统的主密钥或初始密钥一般物理手段发送
  • 对于第3种方法 攻击者一旦获得一个密钥就可获取以后所有的密钥；而且用这种方法对所有用户分配初始密钥时，代价仍然很大。

在单钥密钥体制下有中心的密钥分配和无中心的密钥分配

  • 第4种方法比较常用 其中的第三方通常是一个负责为用户分配密钥的密钥分配中心(KDC)。 这时每一用户必须和密钥分配中心有一个共享密钥，称为主密钥。（可通过第二种方法） 通过主密钥分配给一对用户的密钥ks称为会话密钥，用于这一对用户之间的保密通信。 通信完成后，会话密钥即被销毁。如上所述，如果用户数为n，则会话密钥数为n(n-1)/2。但主密钥数却只需n个，所以主密钥可通过物理手段发送。

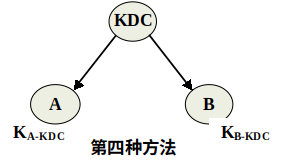
    image-20201202200822401

  • 网络中如果用户数目非常多且分布的地域非常广，则需要使用多个KDC的分层结构

  • 分层结构可减小主密钥的分布，因为大多数主密钥是在本地KDC和本地用户之间共享。

  • 分层结构还可将虚假KDC的危害限制到一个局部区域，但会降低信任度

  • 在基于对称密钥和公钥的密钥管理中都存在分层控制问题

  • 普遍采用的方式是KDC密钥管理体系

    主密钥的分配采用物理的方式，由KDC负责对用户的密钥进行管理，基于第2种方式在用户和KDC之间建立共享主密钥，要求所有用户必需信任KDC，且需要对KDC进行严格的保护。如果系统规模庞大，还要使用分层控制的方式

    用KDC为用户分配密钥时，要求所有用户都信任KDC，同时还要求对KDC加以保护。如果密钥的分配是无中心的，则不必有以上两个要求

  • 无中心的密钥分配时，两个用户A和B建立会话密钥需经过以下3步： ① A向B发出建立会话密钥的请求和一个一次性随机数$N_1$ ② B用与A共享的主密钥$MK_m$对应答的消息加密，并发送给A 应答的消息中有B选取的会话密钥$K_S$、B的身份$ID_B、f(N_1)$和另一个一次性随机数$N_2$ ③ A使用新建立的会话密钥$K_S$对$f(N_2)$加密后返回给B

    image-20201202201407314

单钥体制中密钥控制技术的两种技术

  • 密钥标签
  • 控制矢量

公钥体制下公钥的4种分配方法

  • 主要有两个方面的问题需要解决

    1. 公钥密码体制所用的公开密钥的管理和分配
    2. 如何用公钥体制来分配单钥密码体制所需的密钥，这是公钥加密的主要用途之一

  • 公钥的分配方法主要有以下4种

    1. 公开发布

      公开发布指用户将自己的公钥发给每一其他用户，或向某一团体广播

      缺点很明显，即任何人都可伪造这种公开发布

    2. 公用目录表 公用目录表指一个公用的公钥动态目录表 公用目录表的建立、维护以及公钥的分发由某个可信的实体或组织承担，称这个实体或组织为公用目录的管理员 该方案有以下一些组成部分： ① 管理员为每个用户都在目录表中建立一个目录，目录中有两个数据项: 用户名；用户的公开钥 ② 每一用户都亲自或以某种安全的认证通信在管理者那里为自己的公开钥注册，用户能够直接操作目录表 ③ 用户如果由于自己的公钥用过的次数太多或由于与公钥相关的秘密钥已被泄露，可随时用新密钥替换现有的密钥

      ④ 管理员定期公布或定期更新目录表 ⑤ 用户可通过电子手段访问目录表，这时从管理员到用户必须有安全的认证通信

      安全性高于公开发布，但仍易受攻击 如果敌手成功地获取管理员的秘密钥（密码），就可伪造一个公钥目录表，以后既可假冒任一用户又能监听发往任一用户的消息。(因为公钥目录表的保护不是十分安全) 公用目录表还易受到敌手的窜扰(因为用户亲自操作目录表，可能会破坏目录表) 用户需要登录到公钥目录表中自己查找收方的公钥

    3. 公钥管理机构

      为防止用户自行对公钥目录表操作所带来的安全威胁，假定有一个公钥管理机构来为各用户建立、维护动态的公钥目录 即由用户提出请求，公钥管理机构通过认证信道将用户所需要查找的公钥传给用户 该认证信道主要基于公钥管理机构的签名

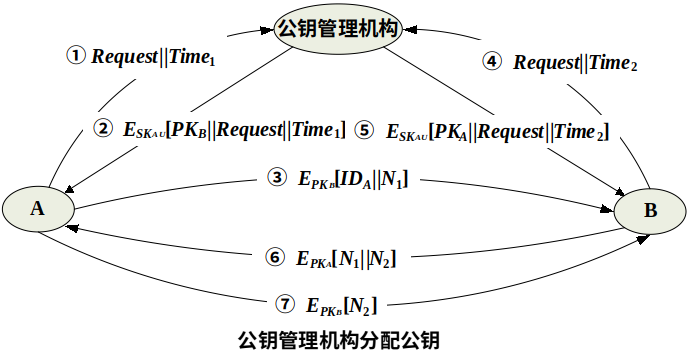
      image-20201202202528052

      • 其中消息②中 管理机构对A的应答消息用自己的秘密钥SKAU加密签名，消息还包含了A的请求，抗篡改、抗重放；包括最初的时戳，抗重放
      • 一次性随机数N1和N2，用于保障通信的新鲜性，使A和B能够完成握手

      公钥管理机构方式的优缺点 每次密钥的获得由公钥管理机构查询并认证发送，用户不需要查表，提高了安全性 但公钥管理机构必须一直在线，由于每一用户要想和他人联系都需求助于管理机构，所以管理机构有可能成为系统的瓶颈 由管理机构维护的公钥目录表也易被敌手通过一定方式窜扰

    4. 公钥证书

      • 用户通过公钥证书来互相交换自己的公钥而无须与公钥管理机构联系

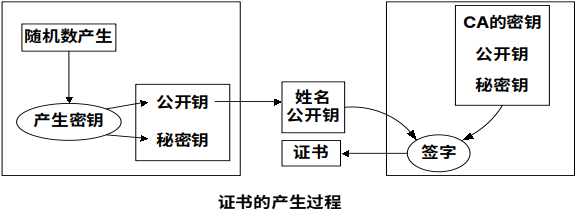
      • 公钥证书由证书管理机构CA(certificate authority)为用户建立

      • 证书中的数据项有与该用户的秘密钥相匹配的公开钥及用户的身份和时戳等，所有的数据项经CA用自己的秘密钥签字后就形成证书

        image-20201202203122807

      • 公钥基础设施PKI(public key infrastructure)是指结合公钥密码体制建立的提供信息安全服务的基础设施

      • PKI技术提供以下四种安全服务 (1) 数据的保密性：保证在开放的网络上传输的机密信息不泄露给非法接受者 (2) 数据的完整性：保证在开放的网络上传输的信息不被中途篡改及重复发送； (3) 身份认证：对通信方的身份、数据源的身份进行认证，以保证身份的真实性； (4) 不可否认性：通信各方不能否认自己在网络上的行为

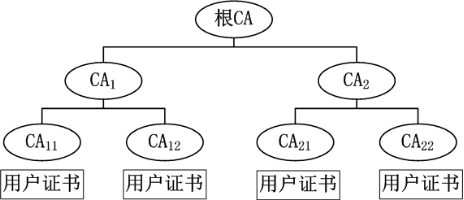
      • 一个PKI系统由认证中心、证书库、Web安全通信平台，RA注册审核机构等组成，其中认证中心CA和证书库是PKI的核心

      • 认证中心CA的体系结构

      • image-20201202203719760

用公钥加密分配单钥体制密钥

  • 简单分配

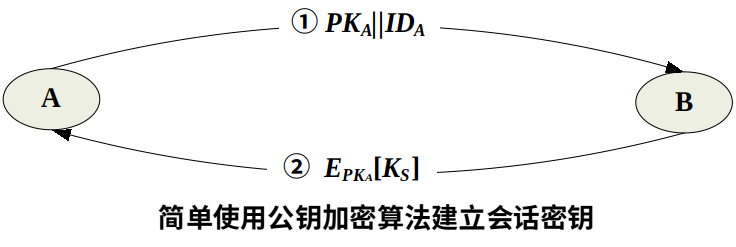
  • image-20201203224128227

  • A、B现在可以用单钥加密算法以KS作为会话密钥进行保密通信，通信完成后，又都将KS销毁 这种分配法尽管简单，但却由于A、B双方在通信前和完成通信后，都未存储密钥，因此，密钥泄露的危险性为最小，且可防止双方的通信被敌手监听, 每次公私钥由发方临时产生 但由于公钥缺少证书管理机构认证且非物理传输容易受到主动攻击

  • 具有保密性和认证性的密钥分配

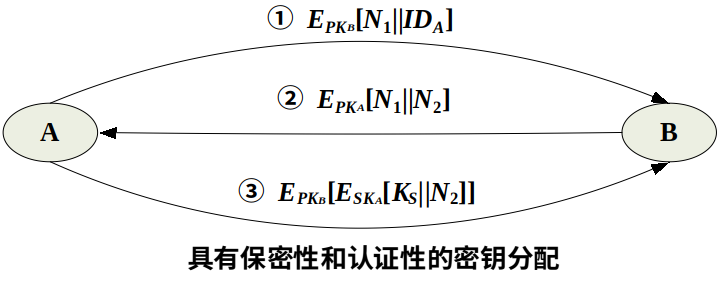
  • image-20201203224409388

Diffie-Hellman密钥交换

  • 上面已经提到

线性同余算法伪随机数生成器及其变形

  • 随机数在密码学中的作用 相互认证中的一次性随机数，如在密钥分配中，都使用了一次性随机数防止重放攻击 会话密钥的产生，用随机数作为会话密钥 公钥密码算法中密钥的产生，用随机数作为公钥密码算法中的密钥，或以随机数来产生公钥密码算法中的密钥

  • 在随机数的各种应用中，都要求随机数序列满足两个特性 随机性和不可预测性 （1）随机性 以下两个准则常用来保障数列的随机性： ①均匀分布 数列中每个数出现的频率应相等或近似相等 ②独立性 数列中任一数都不能由其它数推出

    （2）不可预测性 在诸如相互认证和会话密钥的产生等应用中，不仅要求数列具有随机性而且要求对数列中以后的数是不可测的 对于真随机数列来说，数列中每个数都独立于其它数，因此是不可预测的 对于伪随机数来说，就需要特别注意防止敌手从数列前边的数预测出后边的数

  • 最为广泛使用的伪随机数产生器是线性同余算法 线性同余算法有4个参数： 模数m (m>0)， 乘数a (0<=a<m)， 增量c (0<=c<m)， 初值即种子 $X_0(0<=X_0<m)$； 由以下迭代公式得到随机数数列{ $X_n$}： $X_{n＋1}＝aX_n+c \mod m$ 如果$m，a，c，X_0$都为整数则产生的随机数序列{$ X_n$}也都是整数

  • 评价线性同余算法的性能有以下3个标准： ①迭代函数应是整周期的，即数列中的数在重复之前应产生出0到m之间的所有数 ②产生的数列看上去应是随机的。因为数列是确定性产生的，因此不可能是随机的，但可用各种统计检测来评价数列具有多少随机性 ③迭代函数能有效地利用32位运算实现

  • a, c和m的取值是产生高质量随机数的关键，通过精心选取a, c和m，可使以上3个标准得以满足 为使随机数数列的周期尽可能大，m应尽可能大，普遍原则是选m接近等于计算机能表示的最大整数，为了方便32位运算地实现，m可取为$2^{31}-1$，这满足上述的第③条要求

  • 对第①条来说，一种典型的选取方式是， m为素数、c=0、a是m的一个本原根

  • Knuth给出了使迭代函数达到整周期的充要条件

  • 通常，可取$m＝2^r，a＝2^i＋1，c＝1$，其中r是一整数，i<r也是一整数即可满足定理条件

  • 线性同余算法的强度在于如果将乘数和模数选择得好，则产生的数列和从1，2，…，m-1中随机选取的数列是不可区分的

  • 线性同余算法的密码分析

    给定参数，则线性同余算法由初始值$X_0$确定 如果敌手知道正在使用线性同余算法，并知道算法的参数，则一旦获得数列中的一个数，就可得到以后的所有数 甚至如果敌手只知道正在使用线性同余算法以及产生的数列中极少一部分，就足以确定出算法的参数。假定敌手能确定$X_0，X_1，X_2，X_3$，就可通过以下方程组解出a，c和m。

    $X_1＝(aX_0+c) \mod m$ $X_2＝(aX_1+c) \mod m$ $X_3＝(aX_2+c) \mod m$

    改进的方法是利用系统时钟修改随机数数列 一：每当产生N个数后，就利用当前的时钟值模m后作为种子 二：直接将当前的时钟值加到每个随机数上(模m加)

  • 对线性同余算法有以下一些常用变形

  • 幂形式的迭代公式为$X_{n＋1}＝(X_n)^d \mod m，n＝1，2，…$ 其中d, m是参数，$X_0(0<=X_0<m)$是种子 根据参数的取法，幂形式又分为以下两种：

    ①RSA产生器 此时参数取为RSA算法的参数，即m是两个大素数乘积，d是RSA秘密钥，满足$gcd(d, \phi(m))=1$ ②平方产生器 取d＝2，m＝pq，而p，q模4余3的大素数

  • 离散指数形式的迭代公式为$X_{n＋1}＝g^{X_n} \mod m，n＝1，2，…$ 其中g, m是参数，$X_0(0<=X_0<m)$是种子

ANSI X 9.17 伪随机数生成器的原理

  • 它是密码强度最高的伪随机数产生器之一，已在包括PGP等许多应用过程中被采纳， 产生器有3个组成部分

  • ① 输入 输入为两个64比特的伪随机数，其中$DT_i$表示当前的日期和时间，每产生一个数$R_i$后，$DT_i$都更新一次；$V_i$是产生第i个随机数时的种子，其初值可任意设定，以后每次自动更新。 ②密钥 3次3DES(EDE)加密使用 相同的两个56比特的密钥K1和K2 ③输出 为一个64比特的伪随机数 $R_i$和一个64比特的新种子$V_{i＋1}$

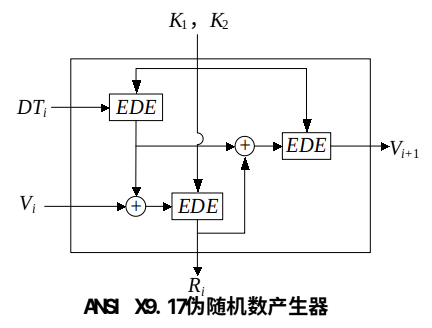
  • image-20201202193436856

  • $R_i＝EDE_{K1,K2}[V_i @ EDE_{K1,K2}[DT_i]]$ $V_{i＋1}＝EDE_{K1,K2}[R_i @ EDE_{K1,K2}[DT_i]]$

  • 本方案具有非常高的密码强度， 这是因为采用了112比特长的密钥和9个DES加密 同时还由于算法由两个伪随机数输入驱动， 一个是当前的日期和时间 另一个是算法上次产生的新种子

  • 前向保密和后向保密性 即使某次产生的随机数$R_i$泄漏了，但由于**$R_i$又经一次EDE加密才产生新种子$V_{i＋1}$**，所以别人即使得到$R_i$也得不到$V_{i＋1}$，从而得不到新随机数$R_{i＋1}$

BBS(blum-blum-shub)随机比特生成器

  • 在某些情况下，需要的是随机比特序列，而不是随机数序列，如流密码的密钥流
  • 首先，选择两个大素数p，q，满足p≡q≡3 mod 4，令n＝p×q。再选一随机数s，使得s与n互素。然后按以下算法产生比特序列{Bi}：
  • image-20201202195322103
  • BBS的安全性基于大整数分解，是密码上安全的伪随机数比特产生器 如果伪随机比特产生器能通过下一比特检验，则称之为密码上安全的伪随机比特产生器 即以伪随机比特产生器的输出序列的前k个比特作为输入，如果不存在多项式时间算法，能以大于1/2的概率预测第k+1个比特。换句话说，已知一个序列的前k个比特，不存在实际可行的算法能以大于1/2的概率预测下一比特是0还是1。

秘密分割Shamir门限方案

  • 设秘密 s 被分成n个部分信息，每一部分信息称为一个子密钥或影子(share or shadow)，由一个参与者持有，使得： ① 由k个或多于k个参与者所持有的部分信息可重构s ② 由少于k个参与者所持有的部分信息则无法重构s 则称这种方案为(k,n)－秘密分割门限方案，k称为方案的门限值。
  • 如果一个参与者或一组未经授权的参与者在猜测秘密s时，并不比局外人猜秘密时有优势,则称这个方案是完善的
  • 攻击者除了试图恢复秘密外，还可能从可靠性方面进行攻击，如果他能阻止多于n-k个人参与秘密恢复，则用户的秘密就难于恢复
  • 秘密分割应该由可信第三方执行，或者托管设备完成
  • Shamir门限方案基于多项式的Lagrange插值公式
  • image-20201202205122395
  • image-20201202205310698
  • image-20201202205327951
  • image-20201202205414985

第六章 消息认证和杂凑算法

消息认证码MAC的定义及三种使用方式

  • 消息认证码MAC指消息被一密钥控制的公开函数作用后产生的、用作认证符的、固定长度的数值，也称为密码校验和
  • 此时需要通信双方A和B共享一密钥k
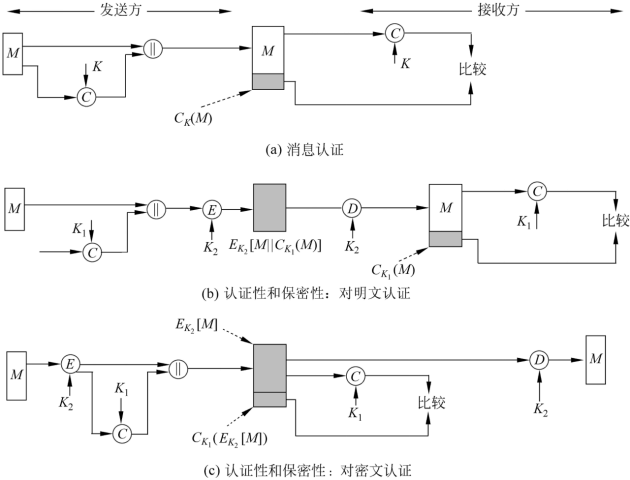
  • image-20201202205920563

ANSIX9.17数据认证算法

  • 算法基于CBC模式的DES算法，其初始向量为零向量 需被认证的数据(消息、记录、文件或程序)被分为64比特长的分组D1，D2，…，DN， 其中最后一个分组不够64比特的话，可在其右边填充一些0，然后按图所示过程计算数据认证码
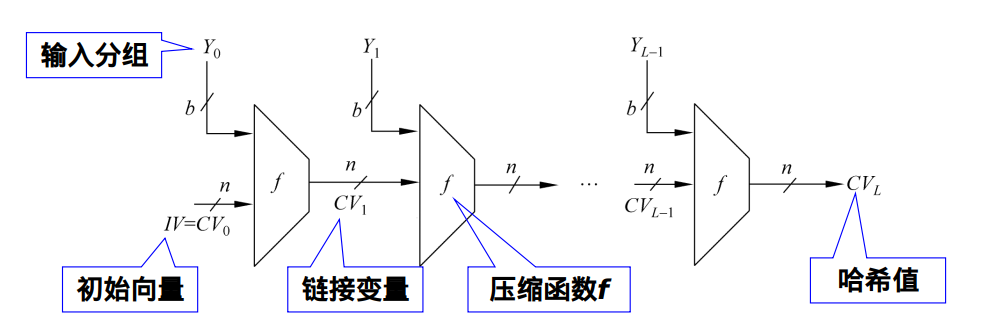
  • 杂凑函数的定义及6种使用方式
  • 迭代型杂凑函数的一般结构
  • image-20201202211223157

MDS和SHA杂凑函数的基本过程, 他们之间的区别与联系

  • 如图所示。其中函数的输入M被分为L个分组Y0,Y1,…,YL-1，每一个分组的长度为b比特，最后一个分组的长度不够的话，需对其做填充
  • 最后一个分组中还包括整个函数输入的长度值，将使得敌手的攻击更为困难
  • IV = 初始值, n =散列码的长度;最后一轮输出的链接变量CVL即为最终产生的哈希值
  • image-20201202211922834
  • MD5算法采用迭代型散列函数的一般结构 算法的输入为任意长的消息，分为512比特长的分组 输出为128比特的消息摘要
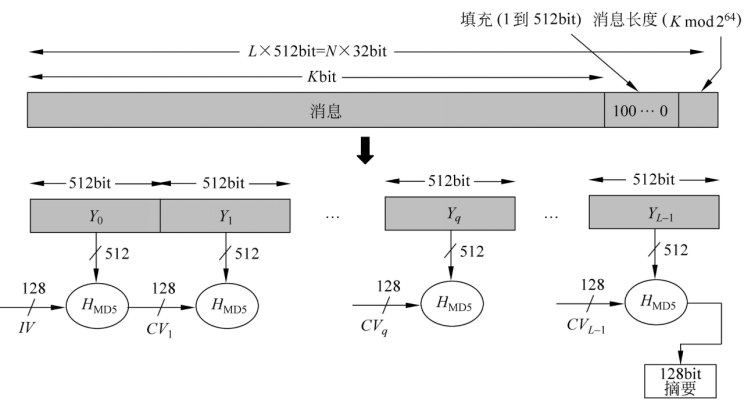
  • image-20201202212059088
  • 处理过程有以下几步： ① 对消息填充，使得其比特长在模512下为448，即填充后消息的长度为512的某一倍数减64，留出的64比特备第2步使用 步骤①是必需的，即使消息长度已满足要求，仍需填充。 填充方式是固定的，即第1位为1，其后各位皆为0
  • 哈希码中每一个比特是所有输入比特的函数 因此获得了很好的混淆效果，从而使得不可能随机选择两个具有相同哈希值的消息
  • SHA-1算法描述
  • 算法的输入为小于264比特长的任意消息，分为512比特长的分组 输出为160比特长的消息摘要。算法的框图与MD5一样，但哈希值的长度和链接变量的长度为160比特
  • ① 对消息填充 与MD5的步骤①完全相同。 ② 附加消息的长度 与MD5的步骤②类似，不同之处在于以big-endian方式表示填充前消息的长度

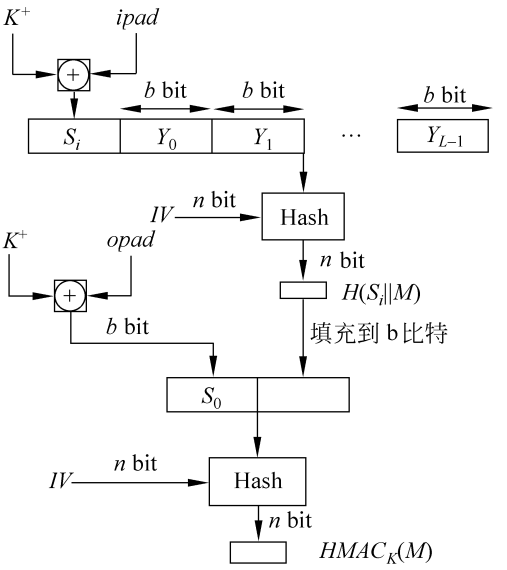
HMAC的算法框图

  • image-20201202212921632
  • image-20201202212930773

第七章 数字签名和密码协议

数字签名的两种产生方式

  1. 由加密算法产生数字签名

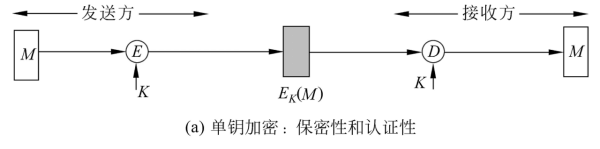
    是指将消息或消息的摘要加密后的密文作为对该消息的数字签名 其用法又根据是单钥加密还是公钥加密而有所不同

    1. 单钥加密，不具备抗抵赖功能 如图：基于共享密钥加解密，密文即为签名 如果加密的是消息摘要或有消息冗余，则可提供消息源认证和完整性认证

    image-20201202213819171

    1. 公钥加密

    然而由于任何人都可使用A的公开钥解密密文，所以这种方案不提供保密性 加密的消息应该是消息摘要或有消息冗余 为提供保密性，A可用B的公开钥再一次加密

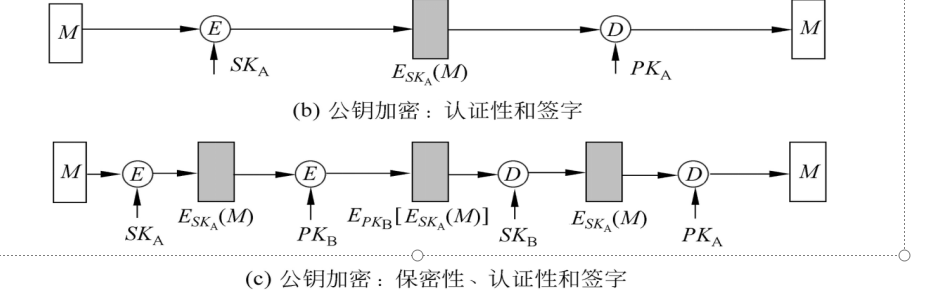
    image-20201202214001365

    由加密算法产生数字签名在实现上一般采用外部保密方式，即先签名后加密，反之则称为内部保密方式 外部保密方式便于解决争议，因为第3方在处理争议时，需得到明文消息及其签名 先签名后加密，可防止签名替换攻击 有时签名消息中还要包含收方的身份 这样可以抵抗假冒攻击

  2. 由签名算法产生数字签名

    image-20201202214315719

数字签名的两种执行方式

  • 数字签名的执行方式有两类： 直接方式和具有仲裁的方式

    1. 直接方式(缺少监督的方式)

      直接方式是指数字签名的执行过程只有通信双方参与，并假定双方有共享的秘密钥或接收一方知道发方的公钥 直接方式的数字签名有一公共弱点，即方案的有效性取决于发方秘密钥的安全性(发方可以声称自己秘密钥被窃取，而否认发过的消息,发方也有秘密钥真的被偷的危险)

    2. 具有仲裁方式的数字签名

      具有仲裁方式的数字签名也有很多实现方案，这些方案都按以下方式运行： ①发方X对发往收方Y的消息签名后，将消息及其签名先发给仲裁者A ②A对消息及其签名验证完后，再连同一个表示已通过验证的指令一起发往收方Y 此时由于A的存在，X无法对自己发出的消息予以否认。在这种方式中，仲裁者起着重要的作用，并应取得所有用户的信任

      image-20201202214831153

RSA签名于DSS签名的不同

  • RSA算法既能用于加密和签名，又能用于密钥交换

  • 与此不同，DSS使用的算法只能提供数字签名功能

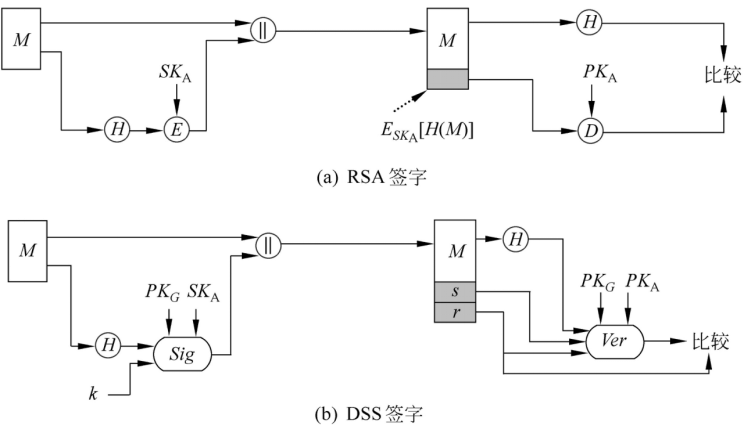
  • image-20201202215234275

  • RSA签名中，先对消息做hash运算，再对hash值用发方的秘密钥加密就形成了对消息的签名

  • DSS签名也先利用杂凑函数产生消息的一个杂凑值，杂凑值连同一随机数k一起作为签名函数的输入

    签名函数还需使用发送方的秘密钥SKA和供所有用户使用的一族参数，称这一族参数为全局公开钥PKG

DSA的算法描述和框图

image-20201204210630136

image-20201204210653014

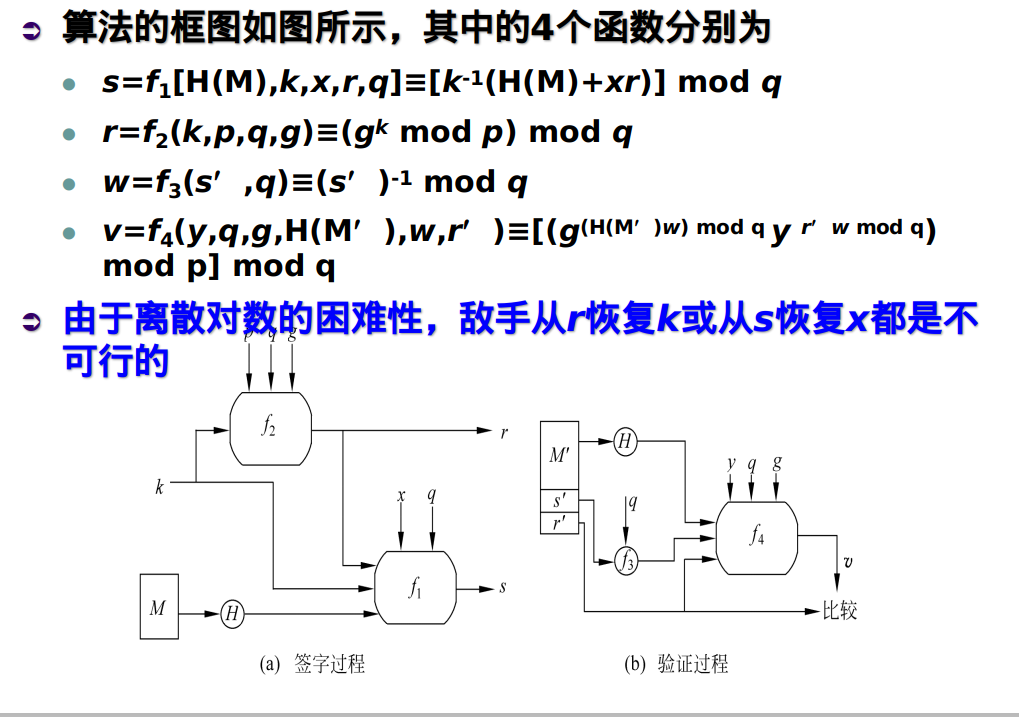
image-20201204210713375

保证消息实时性的两种常用方法

  • 实现消息新鲜性有两种技术：时间戳和询问应答机制
  • 时戳 如果A收到的消息包括一时戳，且在A看来这一时戳充分接近自己的当前时刻， A才认为收到的消息是新的并接受之。这种方案要求所有各方的时钟是同步的
  • 询问-应答 用户A向B发出一个一次性随机数作为询问，如果收到B发来的消息（应答）也包含一正确的一次性随机数，A就认为B发来的消息是新的并接受之。
  • 时戳法不能用于面向连接的应用过程
  • 询问-应答方式则不适合于无连接的应用过程

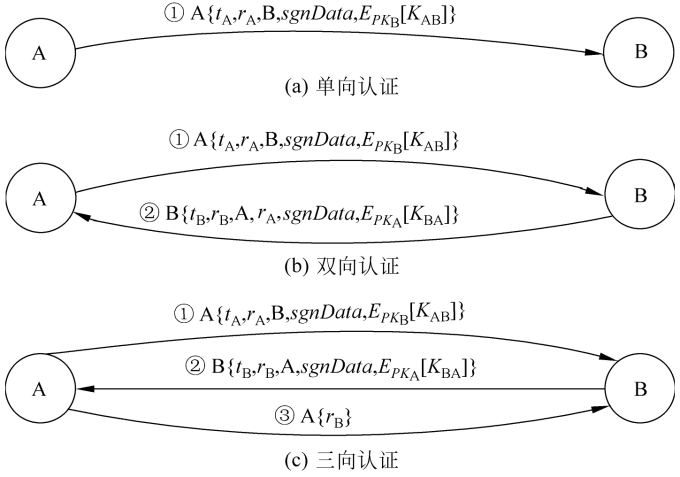
相互认证与单向认证

  • A和B是网络的两个用户，他们想通过网络先建立安全的共享密钥再进行保密通信。A(B)如何确信自己正在和B(A)通信而不是和C通信呢？即双方的身份认证
  • 这种通信方式为双向通信，此时的认证称为相互认证 双向认证也叫相互认证、双方认证等
  • 类似地，对于单向通信来说，认证称为单向认证

交互式证明

  • 交互证明系统由两方参与，分别称为 证明者(prover，简记为P)和验证者(verifier，简记为V)

  • 其中P知道某一秘密（如公钥密码体制的秘密钥或一平方剩余x的平方根），P希望使V相信自己的确掌握这一秘密

  • 交互证明由若干轮组成

    • 在每一轮，P和V可能需根据从对方收到的消息和自己计算的某个结果向对方发送消息
    • 比较典型的方式是在每轮V都向P发出一询问，P向V做出一应答
    • 所有轮执行完后，V根据P是否在每一轮对自己发出的询问都能正确应答，以决定是否接受P的证明

  • 交互证明和数学证明的区别是：

    • 数学证明的证明者可自己独立地完成证明
    • 交互证明是由P产生证明、V验证证明的有效性来实现，因此双方之间通过某种信道的通信是必需的。

  • 交互证明系统须满足以下要求：

    ① 完备性 如果P知道某一秘密，V将接受P的证明 ② 正确性 如果P能以一定的概率使V相信P的证明，则P知道相应的秘密

  • 零知识证明起源于最小泄露证明

    • 如果V除了知道P能证明某一事实外，不能得到其他任何信息，则称P实现了零知识证明，相应的协议称为零知识证明协议

第八章 网络加密与认证

网络加密的两种基本方式

  • 链路加密是指每个易受攻击的链路两端都使用加密设备进行加密
  • 端到端加密是指仅在一对用户的通信线路两端(即源节点和终端节点)进行加密

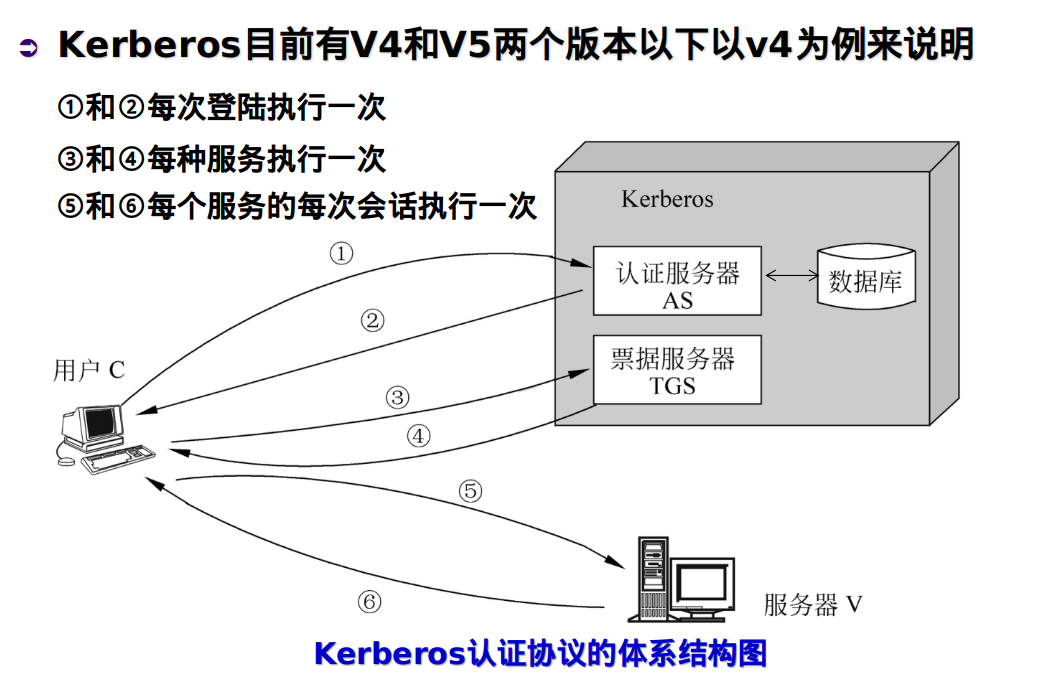
kerberos认证服务系统的详细过程

  • Kerberos协议是工作在应用层的认证协议

  • 解决的问题：

    • 在一个公开的分布式环境中，工作站上的用户希望访问分布在网络中的服务器(可能是多个)上的服务
    • 服务器希望能够限制授权用户的访问，并能对服务请求进行鉴别 Kerberos的主要功能：认证、授权、记账与审计
    • Kerberos系统在一个分布式的Client/Server体系机构中采用一个或多个Kerberos服务器提供一个认证服务
    • Kerberos系统基于对称密钥（DES算法）构建，提供一个基于可信第三方的认证服务

X.509的认证过程

  • 那么如果我们使用证书技术分发公钥的话具体如何做呢？ X.509协议给了我们一个非常实用的标准 X.509协议是X.500系列标准的一个组成部分。 这里X. 500系列标准定义了一种目录业务
  • 目录实际上是维护用户信息数据库的服务器或分布式服务器集合，其中目录中的用户信息包括用户名到网络地址的映射和用户的其他属性，比如互联网中的各个网站名及其网络地址
  • 目录的作用是存放用户的公钥证书
  • X. 509还定义了基于公钥证书的认证协议
  • 目录服务器本身并不负责为用户建立公钥证书，其作用仅仅是为用户访问公钥证书提供方便
  • 认证过程 image-20201202204746674